原文链接:How does SENSE/ASSET work?
- 概要

SENSE(SENSitivity Encoding)和ASSET(Array coil Spatial Sensitivity Encoding)是被最广泛使用的并行成像方法。这些技术主要在从单个线圈重建后的图像空间进行(与此相反,GRAPPA/ARC主要在图像重建前的k空间数据上操作)。主要的MR厂商都提供了不同版本的SENSE技术,有不同的商品名字:Siemens(mSENSE),GE(ASSET),Philips(SENSE),Hitachi(RAPID-“Rapid Acquisition through Parallel Imaging Design”),Toshiba(SPEEDER)。

SENSE/ASSET有四个步骤:
- 产生线圈敏感性映射图;
- 采集部分k空间MR数据;
- 从每个线圈重建部分FOV的图像;
- 通过矩阵求逆展开/合并部分FOV图像。
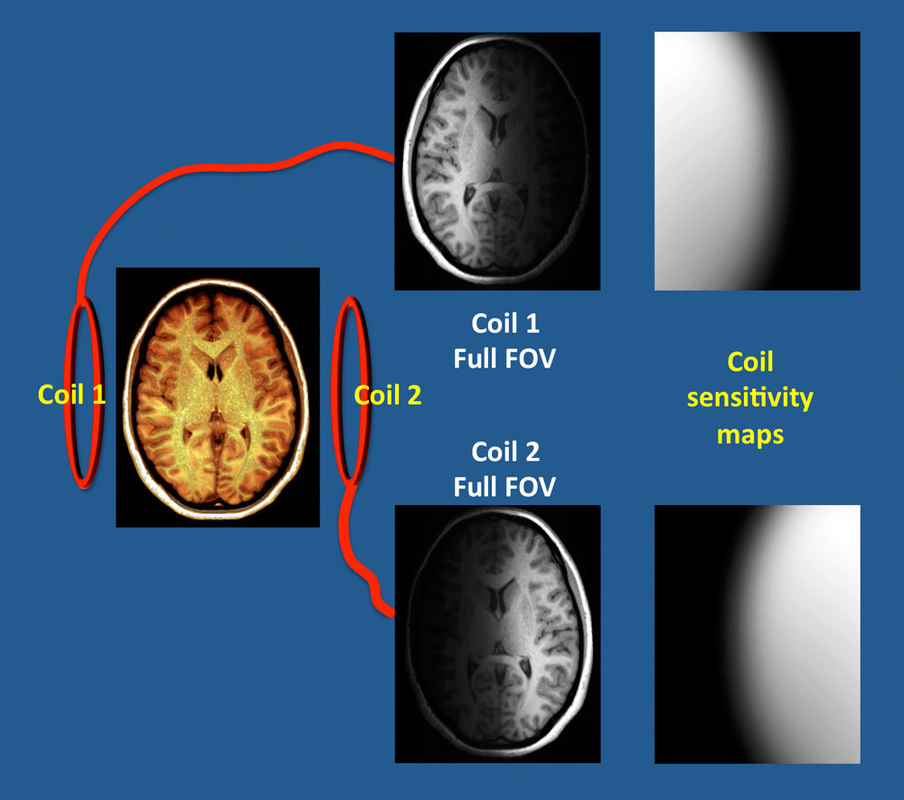
计算线圈敏感性是SENSE技术中第一步也最重要的步骤,使用每个表面线圈单独采集全视野下的低分辨率图像,低分辨率体线圈图像除以这些图像得到归一化数据。然后对这些数据使用滤波,阈值和点估计产生线圈敏感度映射(右图所示)。这些映射图能够量化的表示每个线圈接收区域内来自不同原点信号的相对权重。
线圈敏感性的计算需要在图像实际扫描之前进行,大约花20秒钟(GE的ASSET就使用这种方式)。另外,线圈自动校准也可以集成入脉冲序列本身(Siemens的mSENSE),后一种方法的优势是对发生在校准和扫描开始之间的运动不那么敏感。
一旦线圈敏感性映射图被计算出来,磁共振脉冲序列就开始。假如并行成像的加速因子为2,跳跃采集k空间中交替的行,每个线圈会产生一个½-FOV的卷折图像。矩阵求逆的过程被用于展开和组合从每个线圈获得的混叠图像。此反演过程并不像第一眼看上去那么复杂,2个像素的简单例子如下所示:
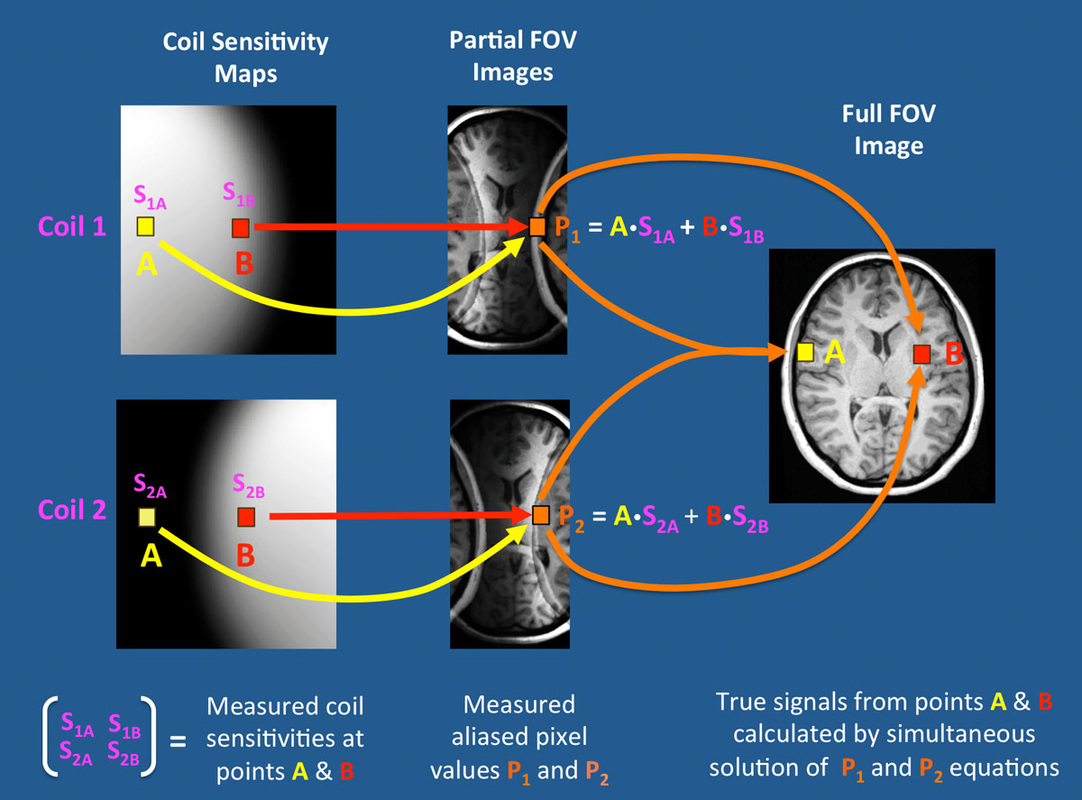
在扫描前的校正阶段,扫描仪为每个表面线圈计算每个点上的敏感性,并且在内存中存储为大的阵列。对于患者A点产生的磁共振信号,线圈1和2检测此信号的敏感性分别记为S1A和S2A,相似的,对另一个点B,线圈1和线圈2的敏感性分别记为S1B和S2B。
每个线圈的数据被重建为图像后会有显著的卷折(折叠)伪影,这种现象称为混叠,是因为成像过程中频率部分的采样数不足以区分所有的空间位置导致的。 ½-FOV图像中的每一个像素点(P)其实是两个点(A和B)的贡献之和。线圈1和线圈2中的这两个像素值分别表示为P1和P2,可以写为:
P1 = A•S1A + B•S1B
P2 = A•S2A + B•S2B
由于Pi和Si都是已知的,真正的信号(A和B)可以通过简单的代数方法计算得到,两个联立的方程组两个未知数。在磁共振扫描仪中会对所有的数据点使用矩阵求逆的技术,与上述过程相似,想法是完全相同的。希望这个例子可以帮助消除围绕SENSE技术重建过程的神秘感。
高级讨论
正如你所预料的,实际中重建过程比上面讨论的要复杂一些。SENSE典型的描述是使用矩阵形式,包含如下部分:I为全FOV下的最终图像,P为有混叠的部分FOV图像,S为每个线圈粗略的敏感性分布,通过体线圈进行归一化,λ为从完整体线圈得到的粗分辨率图像,用于限制正则化过程中的解,ψ为噪声协方差矩阵,表示由具有患者特异性的线圈元素之间相关作用导致的噪声增加。
求逆过程需要解如下的矩阵方程,在图像域使用最小二乘优化:
I = (SHψ-1S + λ-1)-1SHψ-1P
- 参考材料
- Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA. How to choose the optimal method. Top Magn Reson Imaging 2004;15:223-236 [review].
- Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36:55-72. (review)
- Glockner JF, Hu HH, Stanley DW, et al. Parallel MR imaging: a user's guide. Radiographics 2005;25:1279-1297.
- Larkman DJ, Nunes RG. Parallel magnetic resonance imaging. Phys Med Biol 2007;52:R15-R55 [review]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999; 42:952-962.
- 相关问题