原文链接:Why is k-space drawn as a grid? What do the axes in k-space mean?
- 概要

像宇宙外太空一样,k空间也是没有边界的,包含无限多的数据点。为了完美的表示一个物体,需要测量所有的空间频率,要求MR信号的采样有无限的精度,这显然是一个不可能完成的任务。
相反,用于填充k空间的MR信号都被离散采样,然后将这些数据点放置到有限的k空间“网格”(矩阵)中,网格中通常有几千到几十万个单元。每一个数据点(kx, ky)表示一个特定空间频率对图像的贡献。主轴线kx和ky上的点表示图像在x和y方向上的空间频率。不正好在轴上的点表示不同角度上空间频率的贡献。
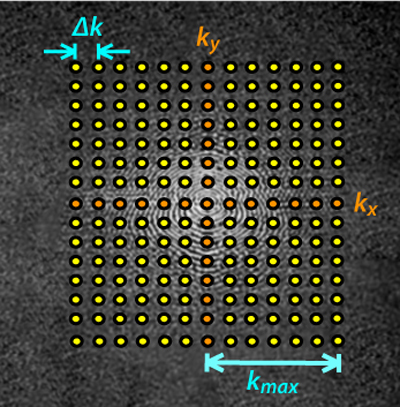
k空间网格通常是正方形的,并且间隔是均匀的,但这并不是必须的。规则的间隔会使得数据采集和处理更容易,更快,更高效。
相邻行或列的距离表示为Δk,k空间中心点到一条边的距离称为kmax。Δk和kmax共同决定最终图像上的像素尺寸和视野(FOV, field-of-view)。这两个参数如何影响图像属性是后续Q&A的主题。
高级讨论
理论上,使用恒定振幅的相位和频率编码梯度对MR信号进行规则采样会将数据放置在规则的正方形矩阵中,如上图所示。但是,数据采样,特别是快速回波或平面回波序列,会在梯度的上升或下降沿时进行。这种情况下,时间上的均匀采样不会产生空间频率上的均匀采样,造成k空间数据被挤到边缘。
出于类似的原因,如果梯度在采集过程中不是恒定的,k空间数据的间隔将是不均匀的。几乎所有的非笛卡尔方法(螺旋,径向,PROPELLER)使用正弦变化的梯度,都会遇到这样的问题。
为了有效地处理非均匀采集的数据,已经开发了许多方法将这些数据做一些“变形”放置到长方形矩阵或“网格”中。这种迭代的过程称为“网格化”。
尽管存在不同的方法,典型的网格化算法首先将原始数据和一组密度补偿量相乘,并与一个网格化核函数卷积,然后对结果数据进行插值,放置到均匀间隔的矩阵(“网格”)中,然后做离散傅里叶变换,最后,对视野进行裁剪,并使用变迹校正函数与变换后的数据相乘。
感兴趣的读者如果想了解更多细节,可以阅读下面参考文献中列出的John Pauly的文章。
- 参考材料
- "Discrete Fourier Transform". Wikipedia, the Free Encyclopedia.
- Pauly J. Non-Cartesian reconstruction. 2005. Available from ee-classes.usc.edu.
- 相关问题