- 概要

普通的物理现象如声波一般没有必要使用负频率描述。比如,“中央C调”的频率为261.63Hz或者电源插座中的电压在60Hz震荡,这样的描述是完全足够的。在这样的场景中,我们将频率考虑为是一个没有符号的标量,有时也称之为时间频率。


在其他情况下,将频率考虑为既有幅度又有方向的矢量更合适。假设有两个轮子,以相同的转速(rpm revolution per minutes,rpm)旋转但是方向不同。这种场景中,对角频率指定正和负(+ω and −ω)以区分顺时针和逆时针方向的运动会更加合理。
傅里叶分析中区分正负频率也很重要,原因是傅里叶变换并不是将一个信号分解为简单的正弦波,实际上,傅里叶变换会将信号分解为复指数函数,可以认为是在两个方向旋转的正弦波和余弦波。
另一个视角看正负频率,回忆一下,频率(ω)即相位(ϕ)随时间(t)的变化速率。在微积分中表示为ω = dϕ/dt(这是有道理的,因为频率的单位可以表示为周期,度或弧度每秒)。
因此正频率(+ω)意味着相位随时间增加,而负频率(−ω)意味着相位随时间减小。
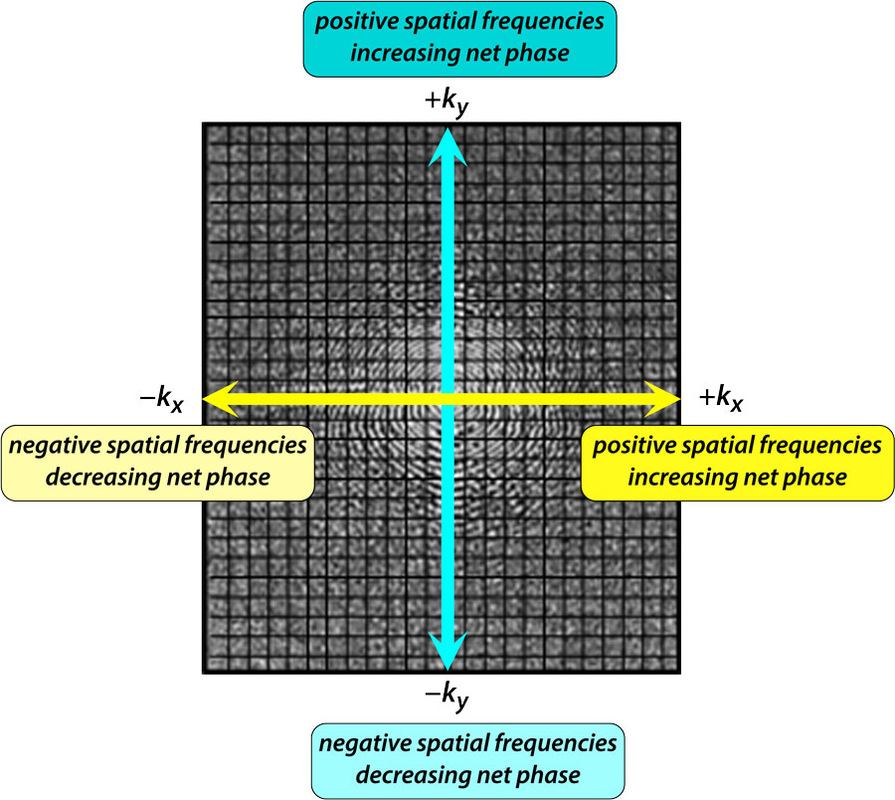
因此−kx和−ky轴对应于负空间频率,也就是累积相位减小。一般情况下,负极性梯度叶会将空间频率和相位“吹向”图表的左侧或下侧(依赖于沿哪个轴施加),相反,一个正极性梯度叶将空间频率和相位“吹向”上方或右方。
- 参考材料
- Johnson, D. Elemental Signals. OpenStax-CNX Web site. http://cnx.org/content/m0004/2.29/, Jul 6, 2009.
- Lyons R. A Quadrature Signals Tutorial: Complex, But Not Complicated. Available at http://www.dsprelated.com/showarticle/192.php
- Negative Frequency. Wikipedia, the Free Encyclopedia.
- Signal Processing Stack Exchange. What is the physical significance of negative frequencies? Available at http://dsp.stackexchange.com/
- 相关问题