Question-信号和空间频率：我不明白你如何将数字化磁共振信号简单地直接插入到k空间中。这些点和空间频率是一致的么？

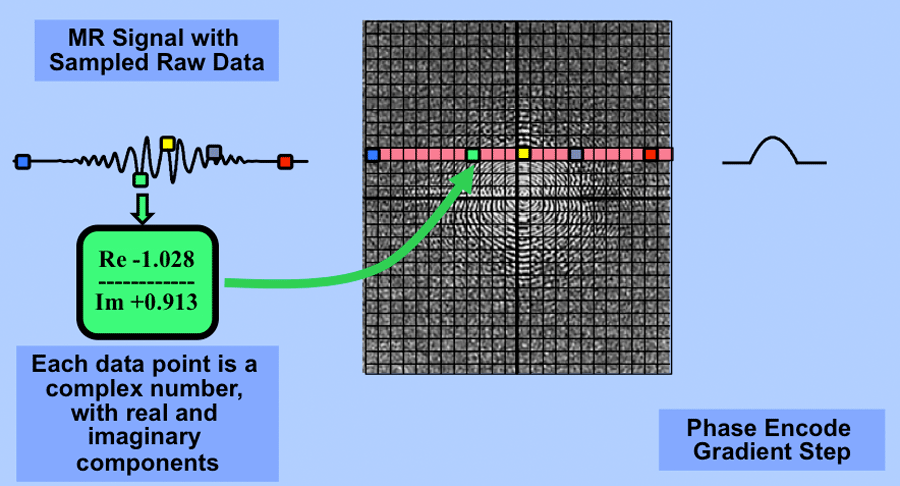
产生MR信号需要施加一个频率编码梯度，回波（或FID，自由感应衰减）中连续采集的数据点反映了逐渐增加的空间频率。这使得从MR信号中采样的原始数据可以直接插入到k空间矩阵中。

换句话说，MR信号的每一个数据点已经是“傅里叶格式”。我称此令人惊讶的事实为k空间的“奇迹”。为什么会发生此奇迹并不非常直观，需要一些解释。

下面的图表显示了一个假想的通过上腹部片层的MR FID信号，此FID信号会因为沿水平轴的失相位梯度G(x)的施加而加速衰减，G(x)既可以是频率编码梯度也可以是相位编码梯度，简化起见，我们假设G(x)随位置(x)线性变化，形式为G(x) = G • x，其中G的单位是mT/m或者等价单位。

当G(x)施加时，给定位置x的总磁场强度为B(x) = Bo + G(x)，此位置相应的共振频率为

f(x) = γB(x) = γBo + γG(x) = fo + γGx

其中γ是旋磁比，fo是主磁场(Bo)的拉莫尔频率。在梯度场施加的过程中，共振频率沿图像从左到右增加。一旦梯度场关闭，共振频率恢复到fo。

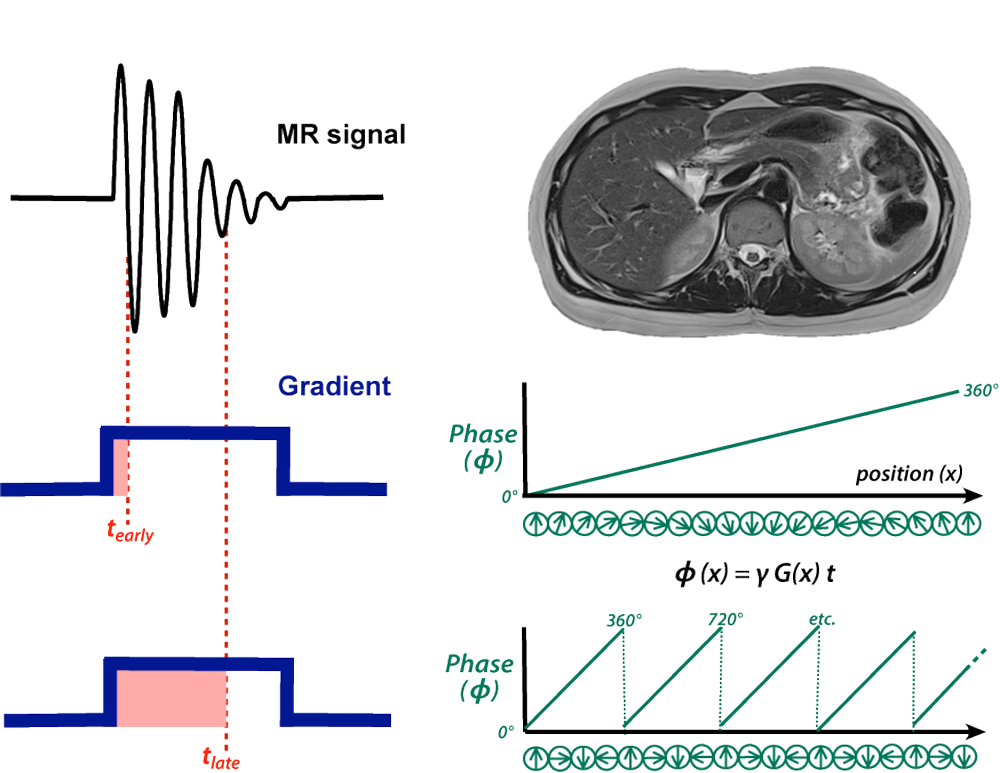
当施加梯度时，磁场更高部分的质子与磁场较低部分的质子相比进动更快，相位增加更多。即使梯度已经关闭，这种相位偏差仍然存在。由于相位 = 频率 x 时间，相位增益与梯度施加时间(t)的长度成正比。相位增益也是位置(x)的函数，表示为：

ϕ(x,t) = (γGx) • t = (γGt) • x = kx(t) • x

其中kx(t) = γGt。这儿的kx就是k空间中的kx，表示沿x方向相位在单位距离内的周期数。

另一种思考k(t)的方法是用旋磁比(γ)乘以梯度(G)曲线在时刻(t)下的面积。虽然像上面简单例子中那样假设线性、矩形的梯度波形沿x轴变化，但是此定义对任意梯度形状和方向(r)也适用。具体而言，

当t = tearly，kx比较小，整个图像的相位传播比较小，当t = tlate，kx比较大并且图像中含多个相位周期。由此在每一个时间点(t)产生的MR信号反映了增加的空间频率和图像中所有位置相位角的加和。因此MR信号中连续的点反映了连续增高的空间频率，其值可以“奇迹般地”直接用于填充k空间。

梯度施加于两个物体，一个均匀(蓝色)，一个具有周期性(红色)。如果相位编码匹配红色物体的周期，将产生一个很强的信号。

如果上面的讨论过于数学化，左边的例子可提供额外的视角。这儿有两个物体，其中一个密度比较均匀（蓝色），另一个密度呈周期性（红色，像一个围栏），两个物体置于相同的梯度场中。假设此梯度会引起两个物体中的一组相移（绿色），其空间频率正好可以匹配红色的物体。

由于均匀物体（蓝色）跨多个相位周期，磁化矢量全部取消，将观测不到任何信号。换句话说，均匀物体中一个相移为φ的像素，很容易找到另一个像素相移为−φ。相反，红色物体在此相位编码中会产生强烈的信号，因为物体固有的空间频率正好可以与梯度产生的空间频率相匹配。

参考材料

相关问题