原文链接:What is a Gibbs artifact?
- 概要

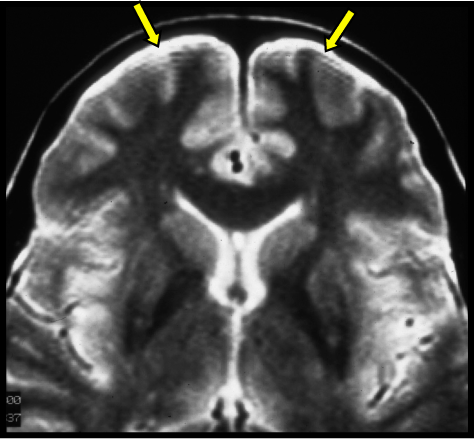
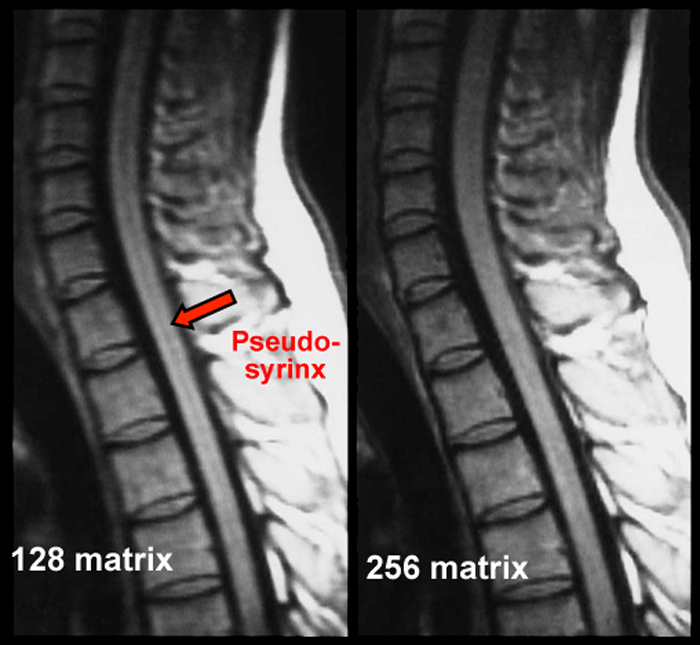
吉布斯伪影(Gibbs artifacts,也称为截断,振铃,或频谱泄露伪影)通常表现为紧邻高对比交界处的多条平行细线。该伪影造成的问题对于脊髓成像尤为严重,会造成脊髓比实际宽或窄,抑或造成脊髓空洞假象。
|
|
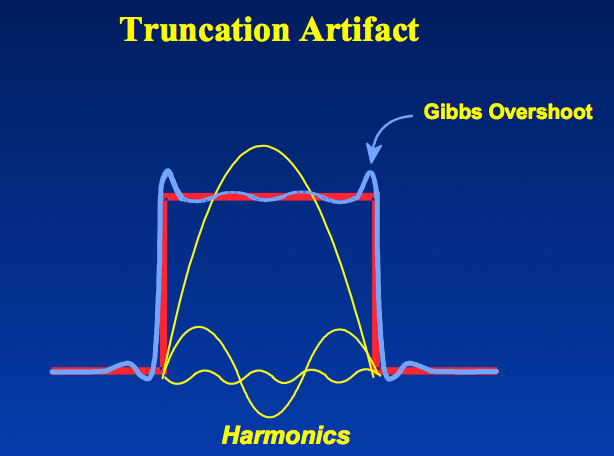
吉布斯伪影是使用傅里叶变换将磁共振信号重建为图像必然的后果。理论上,任何信号都可以用不同幅度,相位和频率的正弦波的无限求和表示。然而在磁共振成像中,仅限制采样有限的频率,也就是用傅里叶表示中相对较少的谐波近似表示图像。傅里叶级数被截断了,这也是该伪影名字的由来。
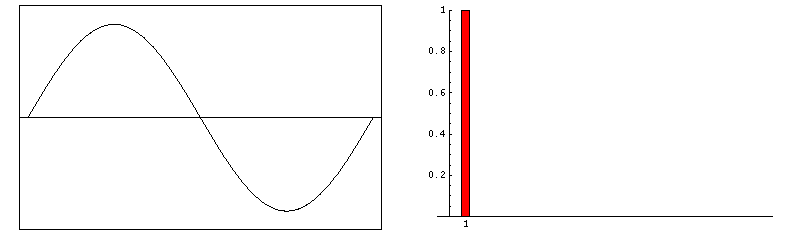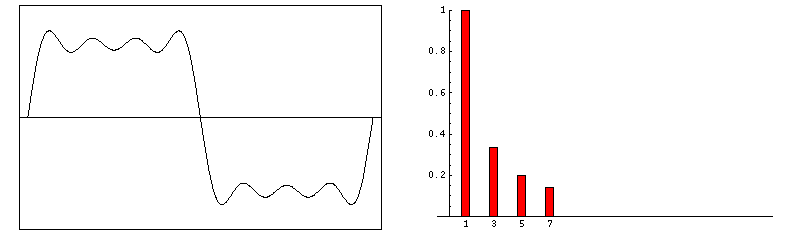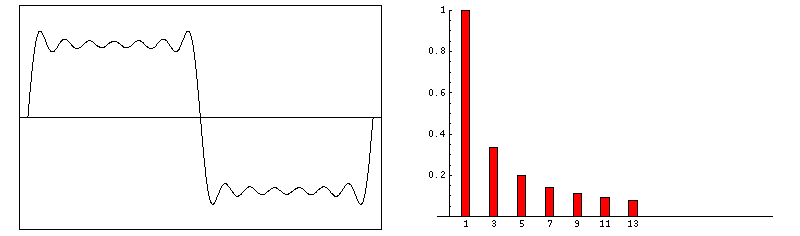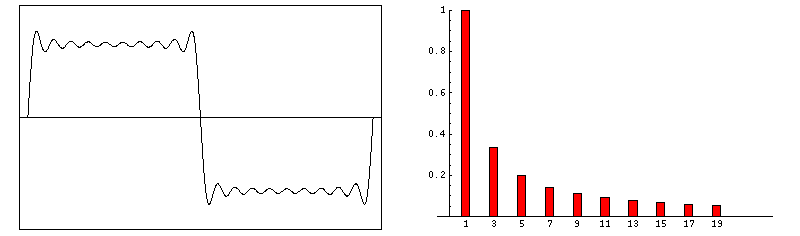
方波的傅里叶合成(Courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State).
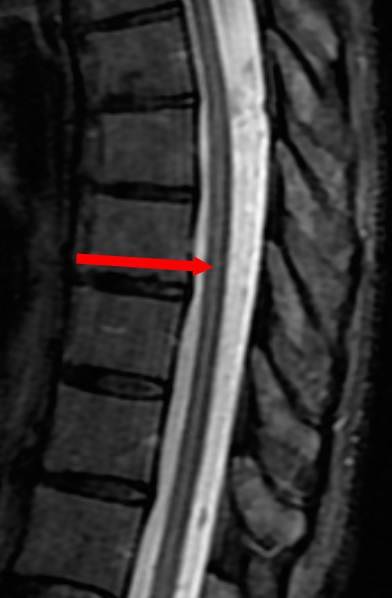
如果物体的信号强度空间上逐渐变化,仅需要很少的几个傅里叶项,截断误差并不明显。然而在高对比度的交界处,傅里叶级数的截断导致明显的伪影,表现为变化的下冲和过冲振荡。取决于贯穿高对比交界处的像素的数目,截断伪影可能有多种形式,包括交界处边缘虚假增宽,交界处边缘增强,或者紧邻交界处的组织扭曲。例如,脊髓中间信号高而边缘信号低(左图)也是截断伪影的另一种表现形式。
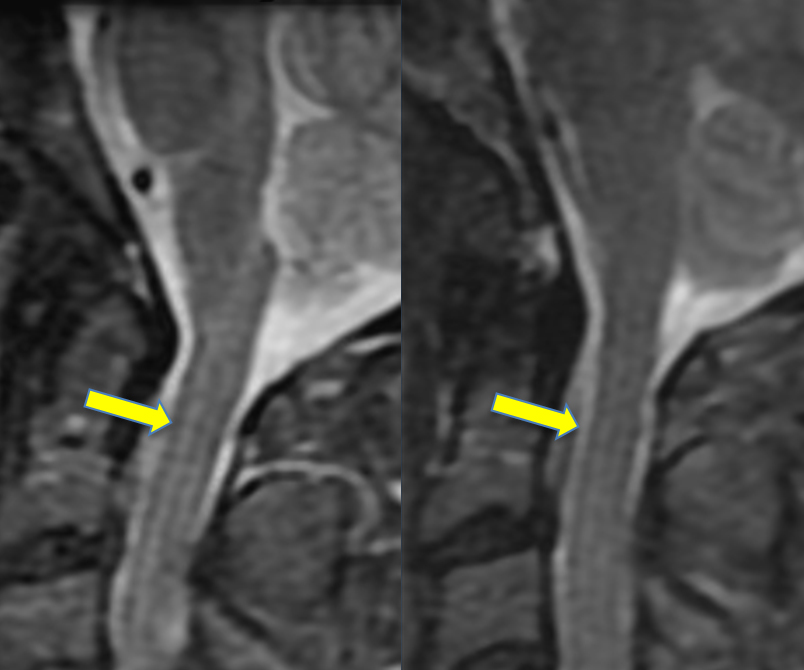
|
|

|

|
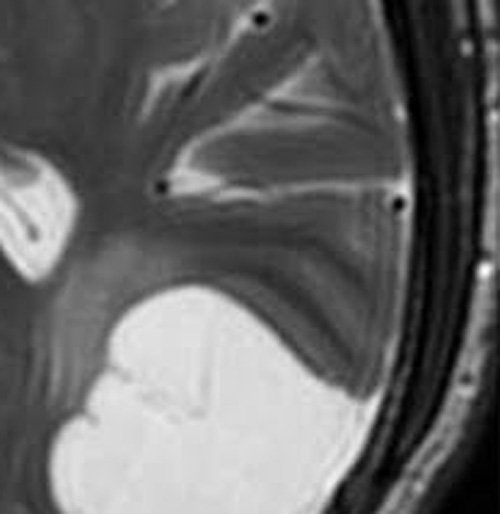
吉布斯(截断)伪影的其他例子
由于截断伪影是图像的傅里叶表示带来的一个基本后果,因此在相位编码和频率编码方向上都会出现。但是相位编码方向上采样数通常更少(如128或192),吉布斯伪影在相位编码方向上通常更显著。最小化截断误差可以通过增加相位编码步数或减小视野达到此目的。但是它们不能被完全消除。
各种方法,在k空间或者后处理操作数据都可以用于最小化截断伪影。被绝大多数厂商采用的一个直接方法是信号处理之前在k空间使用平滑下降的窗(Hamming或Tukey)对信号进行滤波。后处理优化技术,如Total Variation(TV)方法,也可以采用,但是更难实现。所有技术对于减少截断伪影都是有效的,尽管图像质量会略有牺牲。
高级讨论
吉布斯伪影和现象的补充说明
吉布斯(截断)伪影以19世纪数学物理学家Josiah W. Gibbs的名字命名(注意如果使用撇号,须放于“s”后而不是“s”前,也就是Gibbs'而不是Gibb's)。
在他的众多其他科学贡献中(包括热力学中的吉布斯自由能,数学中的向量点乘和叉乘符号),吉布斯研究傅里叶级数不连续时的表现。他描述了在锐利的边缘产生的过冲和振荡,这就是我们现在看到的磁共振图像中的截断伪影。
吉布斯现象一个有趣的数学特征是即使使用无限数目的傅里叶项,波纹会消失,但是在不连续处剩余8.9%的过冲会始终存在。这种不寻常的特征之所以会发生,是因为傅里叶级数是点式的,不会一致性收敛。
磁共振成像中常用的零填充(Zero-flling,ZIP)方法是造成截断伪影的原因。k空间中对低频采样等价于在频率域使用一个矩形采样窗。零填充产生的图像等价于使用一个sinc函数(sinc函数是矩形窗的傅里叶逆变换)与原始图像卷积。如果矩形窗被一个平滑下降的窗(如Hamming)代替,就可以减少截断伪影。
- 参考材料
- Block KT, Uecker M, Frahm J. Suppression of MRI truncation artifacts using total variation constrained data extrapolation. Int J Biomed Imaging 2008; Article ID 184123:1-8.
- Levy LM, Di Chiro G, Brooks RA, et al. Spinal cord artifacts from truncation errors during MR imaging. Radiology 1988; 166:479-483.
- Czervionke LF, Czervionke JM, Daniels DL, Haughton VM. Characteristic features of MR truncation artifacts. AJR Am J Roentgenol 1988; 151:1219-1228.
- 相关问题